
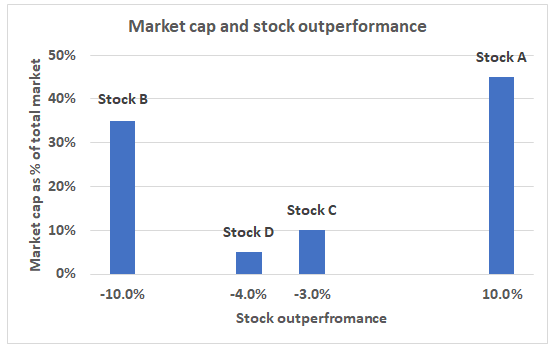
The 3-year annualized ex post standard deviation is calculated using gross returns. The annual composite dispersion presented is an asset-weighted standard deviation (net of fees) calculated for the accounts in the composite the entire year. The portfolio standard deviation is 13.6%. Past performance is not indicative of future results. The portfolio standard deviation after consideration of correlation: S BB = standard deviation of Bits & Bytes S BG = standard deviation of Black Gold and We can illustrate the fact that diversification indeed reduces the risk level by finding the weighted average standard deviation of the investments and then finding the portfolio standard deviation after taking into account the correlation between the two investments. Okoso requested you to calculate for him the extent to which the risk was reduced by the strategy. He started a portfolio with $2,000, invested 50% in Black Gold Inc., an energy company, and 50% in Bits and Bytes, an information technology firm.įollowing statistics relate to these two investments:Ĭorrelation coefficient between returns of BG & B&B is 0.6. In a finance article published in a magazine in those days, he read that the not-all-eggs-in-one-basket approach to investing is useful because it helps reduce risk. A year back he started following the stocks. Multi-Asset Portfolio SD Calculator: Asset Ρ CA = correlation coefficient between returns on asset C and asset A. Ρ BC = correlation coefficient between returns on asset B and asset C. Ρ AB = correlation coefficient between returns on asset A and asset B. Ω B = weight of asset B in the portfolio
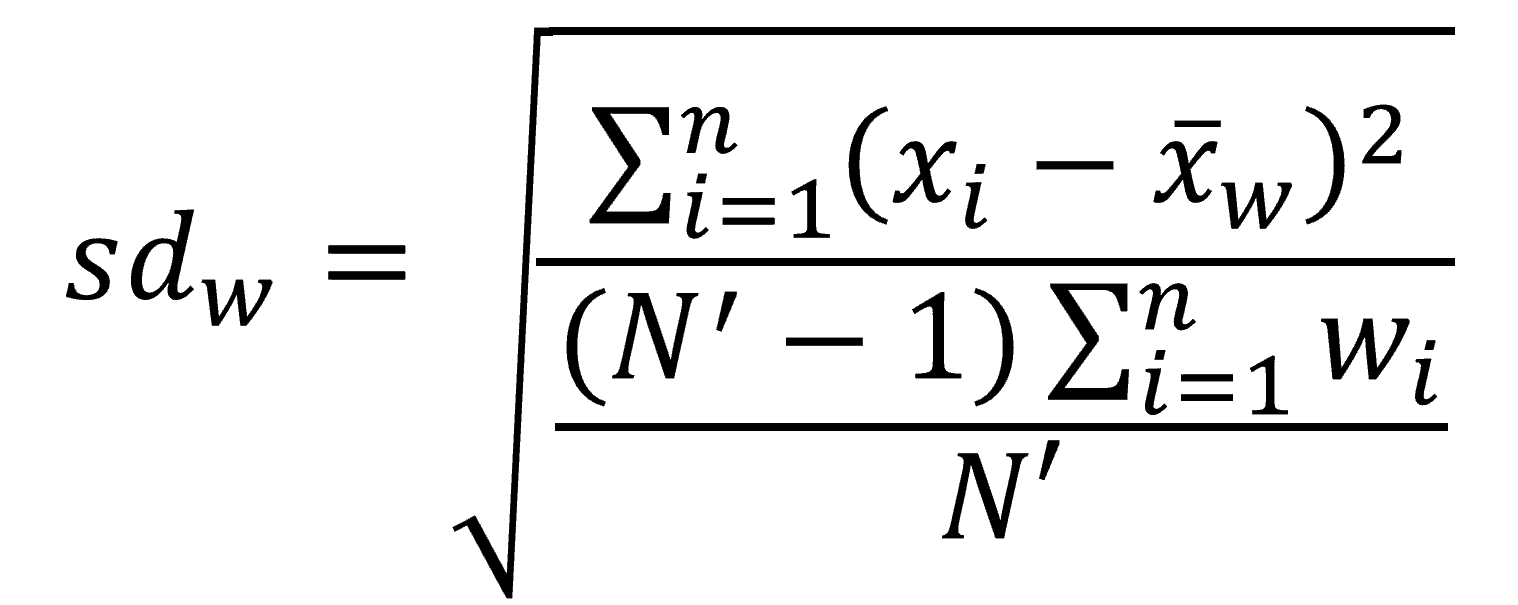
Σ P = is the portfolio standard deviation It is based on the weights of the portfolio assets, their individual standard deviations and their mutual correlation. It is a measure of total risk of the portfolio and an important input in calculation of Sharpe ratio. Σ P = (w A 2σ A 2 + w B 2 σ B 2 + w C 2σ C 2 + 2w Aw Bσ Aσ Bρ AB + 2w Bw Cσ Bσ Cρ BC + 2w Aw Cσ Aσ Cρ AC) 1/2 Portfolio standard deviation is the standard deviation of a portfolio of investments. Portfolio standard deviation for a two-asset portfolio is given by the following formula: Owing to the diversification benefits, standard deviation of a portfolio of investments (stocks, projects, etc.) should be lower than the weighted average of the standard deviations of the individual investments. One of the most basic principles of finance is that diversification leads to a reduction in risk unless there is a perfect correlation between the returns on the portfolio investments. Portfolio standard deviation is the standard deviation of a portfolio of investments.


 0 kommentar(er)
0 kommentar(er)
